１次元井戸型ポテンシャル

量子力学

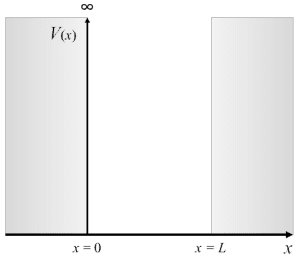
このポテンシャル $V(x)$ は

$$V(x)=\begin{cases}\ 0 \ \ \ \ (0 \leqq x \leqq L) \\ \infty \ \ \ (x<0,\,x>L) \end{cases} \tag{1.1}$$

$x<0,\,x>L$ の領域では $V(x)=\infty$ であり、井戸の外側に出るためには無限のエネルギーが必要となるため、粒子はこの領域に入り込めず $\psi(x)=0$

$0 \leqq x \leqq L$ の領域では $V(x)=0$ となるので、シュレーディンガー方程式は

$$-\dfrac{\hbar^2}{2m}\dfrac{\partial^2 \psi(x)}{\partial x^2}=E\psi(x)\tag{1.2}$$

と表される。この$2$階微分方程式の一般解は

$$\psi(x)=A\sin kx +B\cos kx \tag{1.3}$$

（ただし $k=\dfrac{\sqrt{2mE}}{\hbar}$） で与えられる。$\psi(x)$は複素関数であったから、$A$および$B$は複素定数。

$(1.3)$式の$\psi(x)$に対し、境界条件を適用。未知数は$A$、$B$の２つなので、$\psi(0)=0、\psi(L)=0$を条件として考慮。

$\psi(0)=0$より、$B=0$で、

$$\psi(x)=A\sin kx\tag{1.4}$$

と書ける。また、$\psi(L)=0$ とすると波数$k$について、

$$k=\dfrac{\pi}{L}n\tag{1.5}$$

が必要。ここで$n$は自然数であり、波数$k$は離散値をとることが分かる。ある自然数$n$に対応する$k$を$k_n$として、それに対応して波動関数、エネルギーをそれぞれ$\psi_n(x)$、$E_n$と書く。

$k$の定義式より、

$$E_n=\dfrac{\hbar^2 k_n^2}{2m}=\dfrac{\hbar^2 \pi^2}{2m L^2}n^2\left(=\dfrac{h^2}{8m L^2}n^2\right)\tag{1.6}$$

境界条件だけでは複素係数$A$が定まらないので、以下の規格化条件を利用。

$$\int^{L}_{0}|\psi_n(x)|^2 dx=1\tag{1.7}$$

これに$(1.4)$式を代入。

$$\begin{aligned} & \ \ \ \ \int^{L}_{0}|\psi_n(x)|^2 dx \\ &=\int^{L}_{0}|A\sin k_{n}x|^2 dx \\ &= A^2 \int^{L}_{0}\sin^2 k_{n}x\ dx \\ &= A^2 \int^{L}_{0}\dfrac{1-\cos 2 k_{n}x}{2}\ dx \\ &=\dfrac{A^2}{2} \left[x-\dfrac{1}{2 k_{n}}\sin 2 k_{n}x\right]^{L}_{0} \\ &=\dfrac{A^2}{2} \left\{(L-0)+\dfrac{1}{2 k_{n}}\left(\sin 2n\pi-\sin 0\right)\right\} \\ &=\dfrac{A^2 L}{2} \end{aligned}$$

これより

$$\dfrac{A^2 L}{2}=1$$

となるので、

$$A=\sqrt{\dfrac{2}{L}}\tag{1.8}$$

と求められる。
よってこの系の波動関数$\psi_n(x)$は

$$\psi_n(x)=\sqrt{\dfrac{2}{L}}\sin k_{n}x\tag{1.9}$$